跳转至

Chapter 2 | 二值图像与形态学

约 2429 个字 23 张图片 预计阅读时间 24 分钟

本章概述

二值图像 | Binary image 图像二值化 | Image binarization 形态学操作 | Morphological operation

  • 集合的定义 | Definition of set
  • 腐蚀 | Erosion
  • 膨胀 | Dilation
  • 开运算 | Opening
  • 闭运算 | Closing

应用 | Application

如何从灰度图转为二值图像？ 为什么需要二值图像（实际应用中二值化能把不重要的信息去掉）

Binary Image

灰度图与二值图像的差别如下图所示：

二值图像（Binary Image）中像素（Pixel）的值只有 {0,1} 或者 {0,255}，编程中我们一般用 {0,255} 来构造二值图像。

二值图像的优缺点：

  • 优点：

    • 更小的内存需求
    • 运行速度更快
    • 为二值图像开发的算法往往可以用于灰度级图像

  • 缺点：

    • 应用范围有限；
    • 无法推广到三维空间中
    • 表现力欠缺，不能表现物体内部细节
    • 无法控制对比度

Image binarization

  • 设置一个阈值 Threshold，比阈值小的置为 0, 比阈值大的置为 255.
\[\left\{\begin{matrix}I(x,y)=0\ if\ I(x,y)\leq Threshold \\ I(x,y)=255\ if\ I(x,y)\geq Threshold \end{matrix} \right.\]
  • 如何选取合适的 threshold?

基本思想：将二值化得到的二值图像视为两部分，一部分对应前景（Foreground），另一部分对应背景（Background）。尝试找到一个合适的 threshold 使得到的前景和背景的内部方差最小，而它们之间的方差则最大。（事实上，这二者是等价的）

这就是大津算法的思想

OTSU 大津法

大津法（OTSU）是一种确定图像二值化分割阈值的算法，由日本学者大津于 1979 年提出。从大津法的原理上来讲，该方法又称作最大类间方差法，因为按照大津法求得的阈值进行图像二值化分割后，前景与背景图像的类间方差最大。

原理推导

OTSU 算法的本质思想就是最大化类间方差

从目的来看我们想设置一个阈值 \(\tau\) 将图像中的像素分为 \(A\)( 大于 \(\tau\))、\(B\)( 小于 \(\tau\)) 两类。那么我们这个阈值的取值范围就是 \([0,255]\)。这里我们取整数，在这 256 个数中选取一个作为我们分割图像的阈值

怎么选取这个阈值呢？我们从代码层面来说

先统计图形中每个灰度的像素个数，设 \(n_i\) 为图像中灰度为 \(i\) 的像素的数量，则有 \(n_0,n_1,n_2...n_{255}\)

图像中像素灰度为 \(i\) 的概率为 :

\[ p_i=\frac{n_i}{n_0+n_1+...+n_{255}} \]

且有：

\[ \Sigma _{i=0} ^ {255} p_i = 1 \]

此时根据 OSTU 的思想来看，我们应该找出一个 \(\tau\) 使得 A、B 两类的方法最大。者可以看成一个求最大值的问题，用 \(\tau\) 遍历 0-255 所有的整数，求出所有对应的方差，取最大方差对应的 \(\tau\)

那现在唯一的问题就是已知 \(\tau\) 和图像，如何求 A 与 B 的方差了

设阈值为 \(k\) 时，像素被分到 A 的概率为 \(p_A(k)\)、分配到 A 的像素的平均灰度为 \(m_A(k)\)

同理设像素被分到 B 的概率为 \(p_B(k)\)、分配到 B 的像素的平均灰度为 \(m_B(k)\)

还有灰度级 \(k\) 的累加均值 \(m \triangleq \Sigma _{i=0} ^k ip_i\)，整个图像的灰度值 \(m_G \triangleq \Sigma _{i=0} ^{255} ip_i\)

则有：

\[ p_A(k) * m_A(k) + p_B(k) * m_B(k) = m_G \tag{1} \]
\[ p_A(k) + p_B(k) = 1 \tag{2} \]

根据方差的概念，方差的表达式写成：

\[ \sigma^2 = p_A(k)(m_A(k)-m_G)^2 + p_B(k)(m_B(k)-m_G)^2 \tag{3} \]

将 (1) 带入 (3):

\[ \sigma^2 = p_A(k)p_B(k)(m_A(k)-m_B(k))^2 \tag{4} \]

其中：

\(p_A(k) = \Sigma_{i=0}^k p_i\) \(p_B(k) = \Sigma_{i=k+1}^{255} p_i\)

\(m=\Sigma_{i=0}^k ip_i\) \(m_G=\Sigma_{i=0}^{255}ip_i\)

\(m_A(k)=\frac{\Sigma_{i=0}^k ip_i}{p_A(k)}\) \(m_B(k)=\frac{\Sigma_{i=k+1}^{255} ip_i}{p_B(k)}\)

当然，为了尊重原著我们可以把 (4) 写成

\[ \sigma^2 = \frac{(m_G*p_A(k)-m)^2}{p_A(k)(1-p_A(k))} \tag{5} \]
  • 过程简述
    • Step 1: 确定原始图像中像素灰度的最大值和最小值；
    • Step 2: 最小值加 1 作为 threshold 对原始图像进行二值化操作；
    • Step 3: 根据对应关系确定前景和背景，分别计算当前 threshold 下的内部协方差和外部协方差；（算一个就可以了）
    • Step 4: 回到 Step 2 直到达到像素最大值；
    • Step 5：比较找到最大外部和最小内部协方差对应的 threshold.

我们可以将前述 thresholding 策略推广到彩色图像，同时考虑 rgb 三个通道，我们就可以针对特定的色彩进行 thresholding 操作 ( 思想类似，但是具体操作暂略 )

Example

大津算法存在问题：全局进行二值化操作不给力，如中间这幅图。

我们可以采用局部自适应操作来优化成为右边的图。具体思想：设定一个局部窗口，在整个图像上滑动该窗口；对于每一窗口位置，确定针对该窗口的 threshold。

Morphology Operation

Morphology

  • 形态学 Morphology

    1960s 后期提出，研究动植物的结构与形态。形态学一般指生物学中研究动物和植物结构的一个分支

  • 数学形态学 Mathematical morphology

    基础理论：集合论。采用一种简单的非线性代数算子，主要用于二值图像，可扩展到灰度图像。用在噪声过滤、形状简化、细化、分割、物体描述等

用数学形态学（也称图像代数）表示以形态为基础对图像进行分析的数学工具

  • 基本思想是用具有一定形态的结构元素 (structure element) 去度量和提取图像中的对应形状以达到对图像分析和识别的目的。
  • 形态学图像处理的数学基础和所用语言是集合论。
  • 形态学图像处理的应用可以简化图像数据，保持它们基本的形状特性，并除去不相干结构。
  • 形态学图像处理的基本运算有 4 个：膨胀、腐蚀、开操作和闭操作

Set Theory for Image

For reference

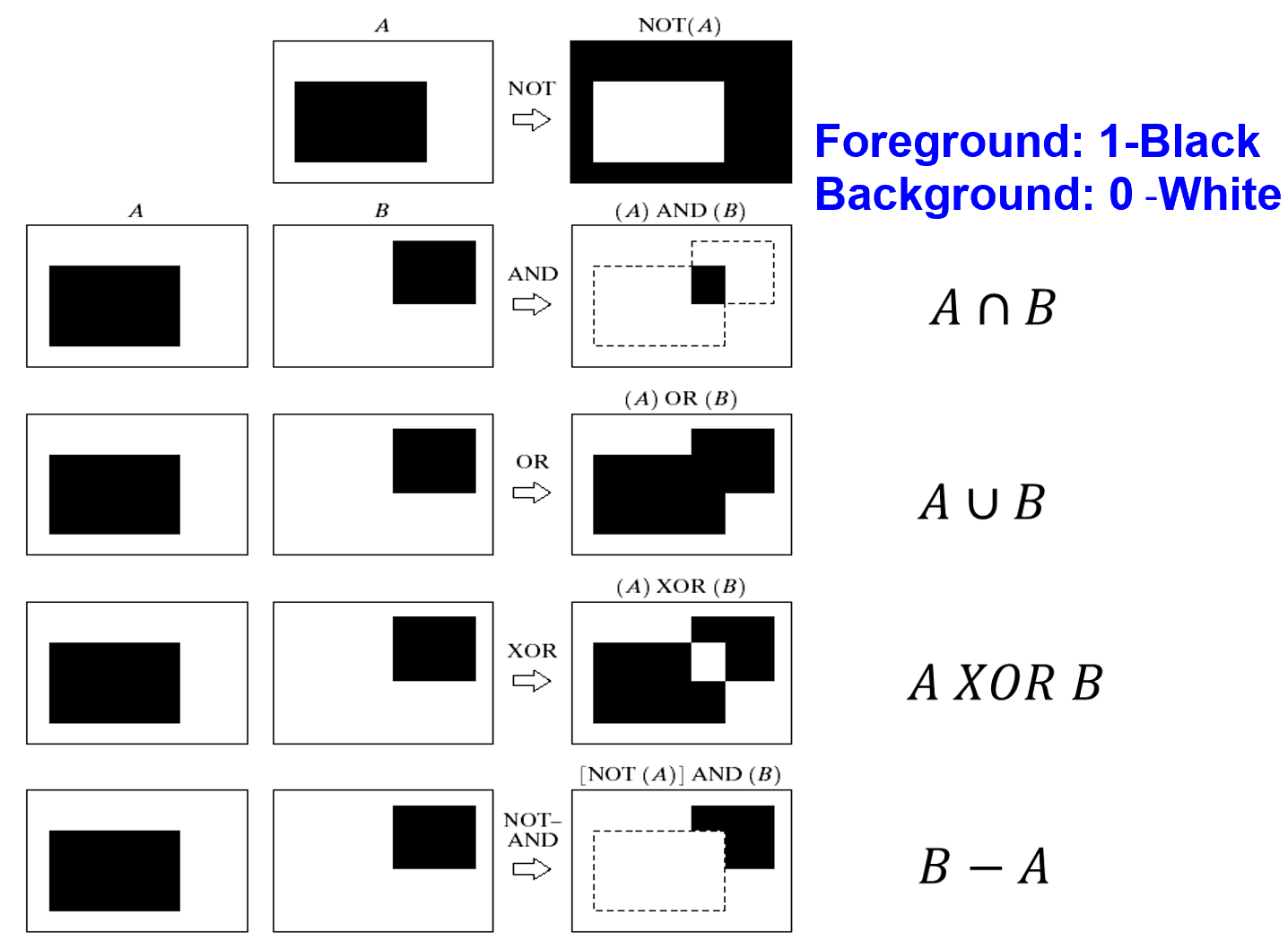
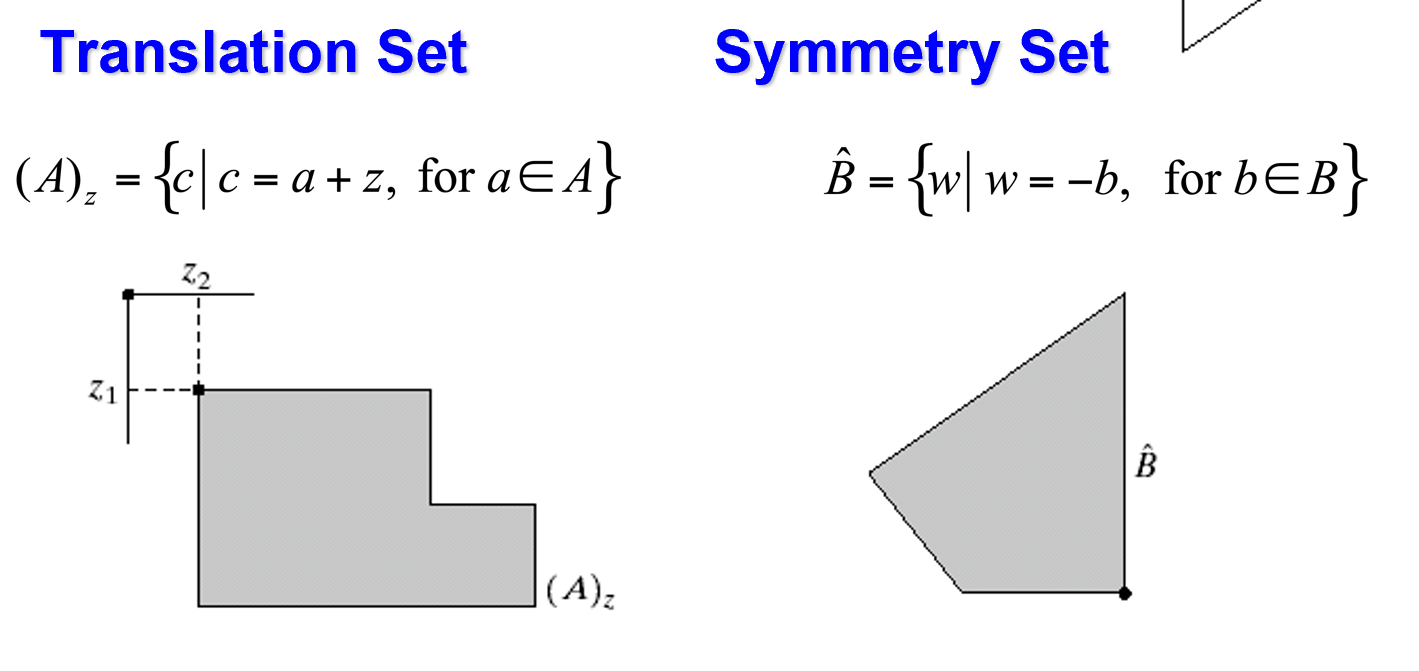
膨胀 | Dilation

膨胀是将与物体“接触”的所有背景点合并到该物体中，使边界向外部扩张的过程。可以用来填补物体中的空洞。（其中“接触”的含义由结构元描述）

\[ A\oplus B = \{(x,y)| (B)_{(x,y)} \cap A \neq \varnothing \} \]

其中 A：二值图像；B：二值模板，称为结构元（structure element）

该式 B 对 A 膨胀，注意这里的 \(\oplus\) 不是异或的意思

膨胀的方法简单来说就是将 B 的中心遍历放置在图像 A 中所有像素点，如果 B 与 A 没有任何接触，那么这个点不作为扩张点，否则这个点就作为扩张点

Dimension 1

Dimension 2

这里的图中第二行的格子有些大，具有一定的误导性

显然我们发现，选择不同形状的结构元，结果也不同。一般来说，我们更多地选择各向同性（即对称）的结构元

腐蚀 | Erosion

腐蚀是一种消除边界点，使边界向内部收缩的过程。可以用来消除小且无意义的物体。

同理

\(A\): Binary image

\(B\): binary template, structure element

\[A\ominus B=\{(x,y)|(B)_{xy}\subseteq A\}\]

Physical meaning: remove boundary, remove unwanted small objects.

腐蚀的做法简单来说，就是将结构元 B 遍历 A 的每一个像素，只有 B 被 A 完全包含的像素才不会被腐蚀

Dimension 1

Dimension 2

Padding

可能有人会有疑问，加入我们的扫描从第一行开始，结构元可能就超出了图像的边界（例如十字形的结构元），这个时候应该如何处理？我们可以借用 padding 的思想：把这一行往上复制一遍，再进行扫描。

Application for Erosion

滤波

这里我们腐蚀了白色像素

提取边界

补洞

接下来我们对膨胀和腐蚀做一个小的总结：

Dilation and Erosion

  • 膨胀
    由B对A膨胀所产生的二值图像D是满足以下条件的点(x,y)的集合：如果B的原点平移到点(x,y)，那么它与A的交集非空。
  • 腐蚀
    由B对A腐蚀所产生的二值图像E是满足以下条件的点(x,y)的集合：如果B的原点平移到点(x,y)，那么B将完全包含于A中
  • 膨胀与腐蚀是对偶的
    \((A\ominus B)^c=\{z|(B_z)\subseteq A\}^c=\{z|(B_z)\cap A=\varnothing\}^c=\{z|(B_z)\cap A^c \neq \varnothing\}=A^c\oplus B\)

开运算 | Open

先腐蚀，后膨胀 \(A\circ B=(A\ominus B)\oplus B\)

Remove small objects, segment object at thin part, smooth boundary of large object but preserve its original area.

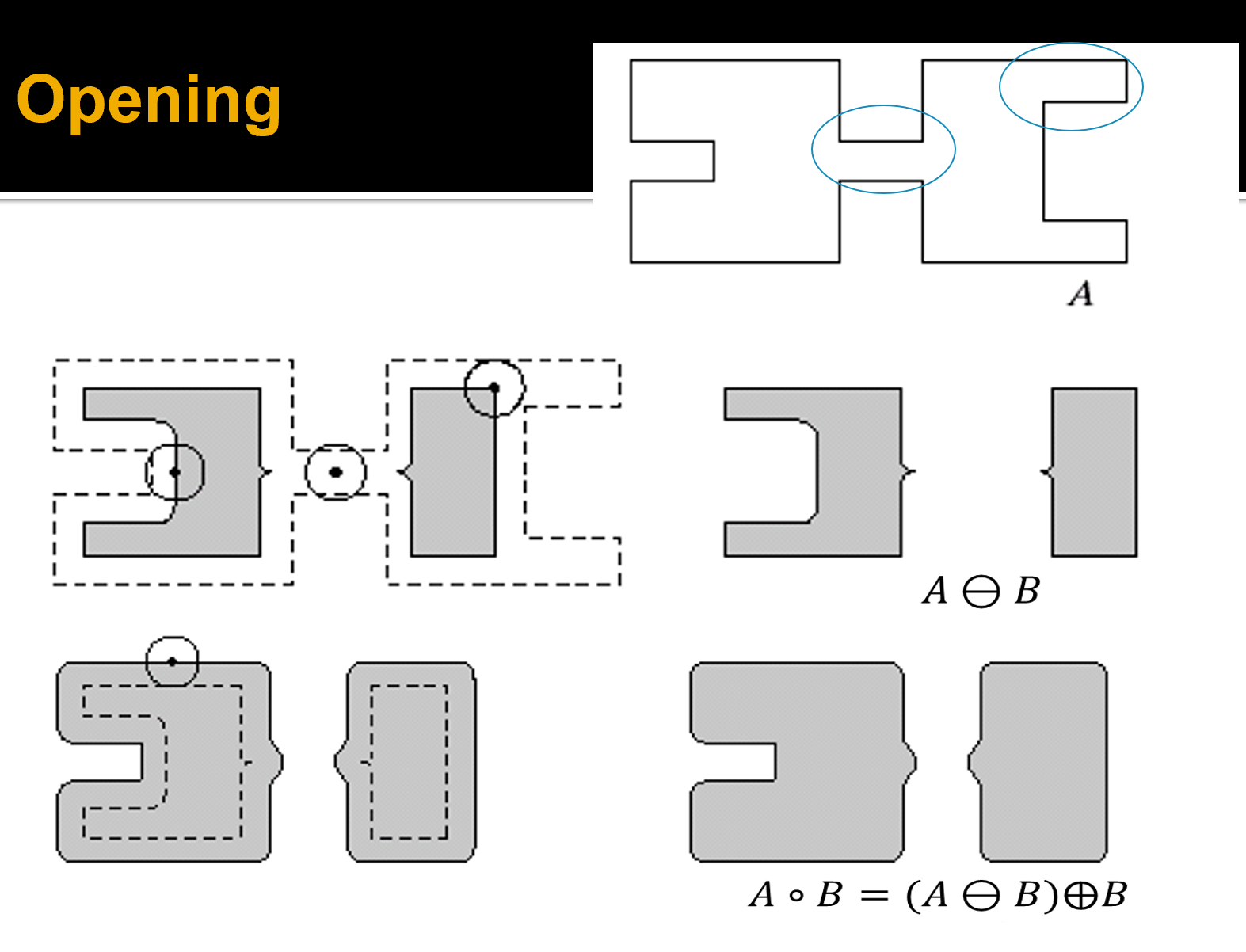
image.png

闭运算 | Close

先膨胀，后腐蚀 \(A \bullet B =(A\oplus B)\ominus B\)

Fill small holes, connect the neighboring objects, smooth boundary while preserving the area at most.

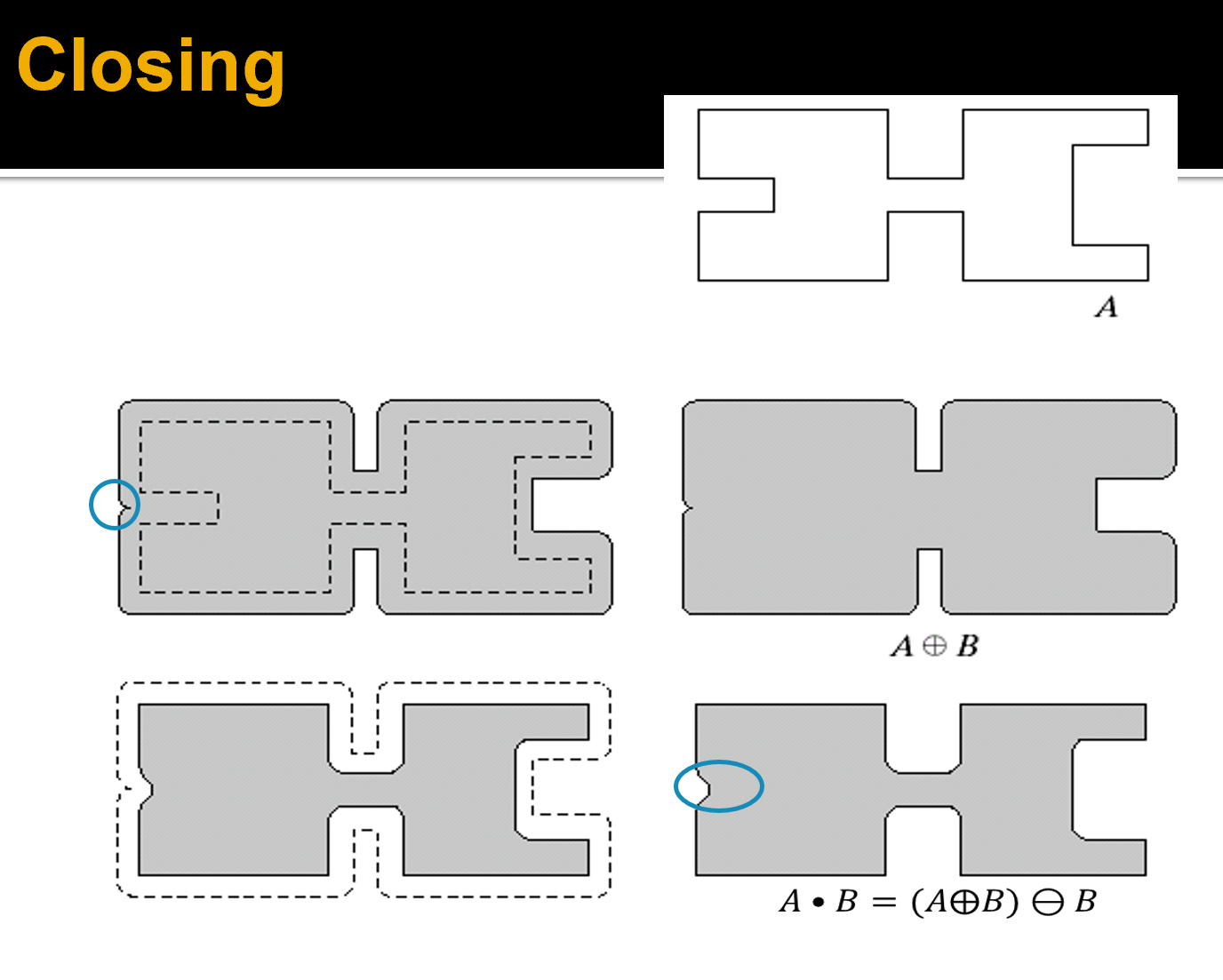
image.png

操作 定义 主要功能 适合处理的情况
开运算 (Open) 先腐蚀再膨胀 去除小前景噪声，平滑物体边缘 适合去除细小的白色前景噪声，平滑前景边缘
闭运算 (Close) 先膨胀再腐蚀 填充小孔，连接断裂部分，平滑边缘 适合填补前景中的小黑色空洞，连接前景物体

总结